Llama-Polya: A Math Tutor LLM

Project Overview

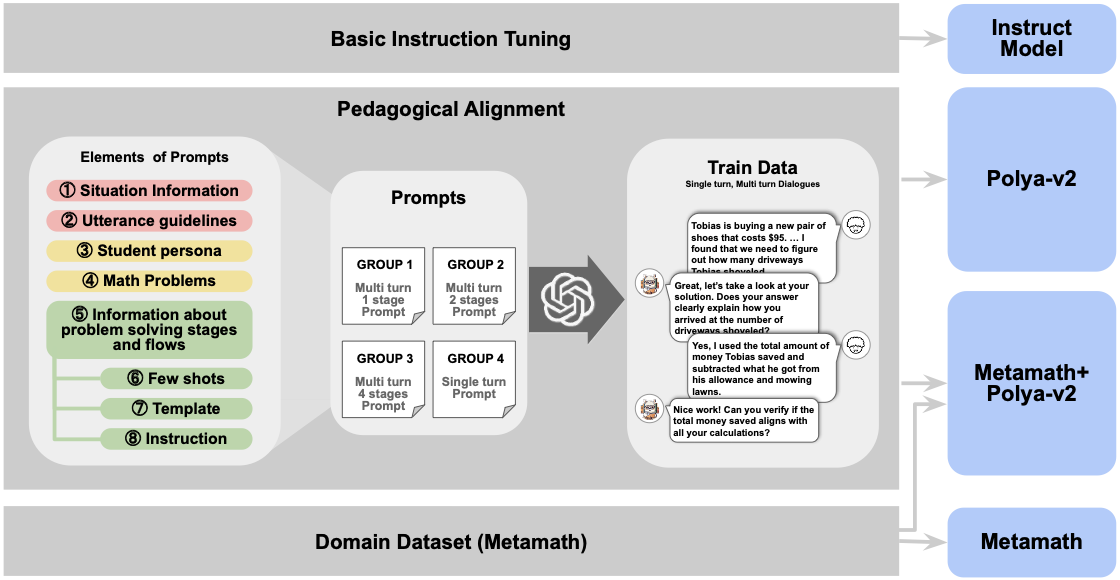
This project introduces Llama-Polya, an instruction-tuned large language model grounded in Polya's four-step problem-solving framework to foster structured mathematical thinking. The model was built on the open-source Llama architecture and fine-tuned on the GSM8K dataset to generate educational context-aware, step-by-step guidance aligned with learners' queries.

Evaluation showed that pedagogically aligned models like Llama-Polya guided learners through reflective, step-by-step reasoning rather than simply providing answers. Models fine-tuned with Polya's problem-solving framework (Polya-v2) and domain knowledge (Metamath) achieved more balanced performance and lower error rates than general-purpose versions. Expert reviewers noted that Llama-Polya supports metacognitive reflection and self-regulated learning, helping students think more critically with AI. This work demonstrates how instruction tuning grounded in educational theory can align LLMs with authentic pedagogical goals and practices.

*This work is under review at IEEE Transactions on Education.

---

Problem We Found

Despite rapid advances in large language models (LLMs), most educational applications remain pedagogically shallow. Current models are optimized for general reasoning or answer generation, not for instructional dialogue that aligns with how humans learn. In mathematics education, this often means that LLMs provide direct solutions instead of supporting learners through the process of understanding, planning, solving, and reflecting—the core of effective problem-solving.

---

Our Approach

We framed math problem-solving as a structured sequence of stages by adopting Polya's four-step framework (understand, plan, carry out, review) as a theoretical anchor. Then, we developed the Llama-Polya following the process illustrated in the figure above.

LLM performance can vary significantly across model variants even when trained on the same data. Therefore, we implement and compare five versions built on different Llama bases:

• base — Standard Llama foundation model
• instruct — Instruction-tuned variant
• polya-v2 — Fine-tuned with Polya's framework
• metamath-polya-v2 — Combined domain knowledge + Polya framework
• metamath — Mathematics-focused variant

These variants let us examine how architectural and fine-tuning choices affect the pedagogical alignment of LLMs.